Функции 3-х переменных
Для минимизации функций, зависящих от трех переменных, применяется следующая диаграмма:
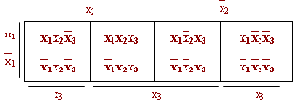
Из диаграммы видно, что склейке подлежат все произведения, расположенные в соседних клетках, а также в клетках, расположенных на краях диаграммы. Результат склейки – есть произведения, содержащее на одну букву меньше. Видно также, что возможна и дальнейшая склейка, однако уже между произведениями, расположенными во взаимно перпендикулярном направлении.
Рассмотрим, например, левую половину диаграммы:
| x1x2x3 | x1x2x3 |
| x1x2x3 | x1x2x3 |
Склеим попарно произведения, стоящие в строках:
| x1x2 | x1x2 |
| x1x2 | x1x2 |
Теперь видим, что можно произвести дальшейшую склейку, но произведений, стоящих в столбцах матрицы:
| x2 | x2 |
| x2 | x2 |
Как видно, результат склейки – произведение x2. Именно эта переменная покрывает все четыре конституенты единицы СДНФ функции.
Подобное же утверждение справедливо и для конституент, расположенных в строках и столбцах диаграммы по краям таблицы.
Таким образом, при поиске минимальной формы необходимо считать левый край таблицы склеенным с правым. Говорят, что для наглядности можно условно данную диаграмму представить нанесенной на поверхность цилиндра.
Пример:
f(x1x2x3) = x1x2x3

x1x2x3



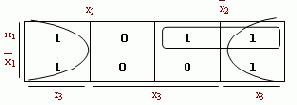
fmin(x1x2x3) = x3

Видим, что две единицы, соответствующие конституентам x1x2x3 и x1x2x3, покрываются произведением x1x2.
